問1

問1/解説
- 高度間隔ごとに一定の比率で減少
- 大気全体の質量の99.9%

まずはじめに問題文の中にある上記のPOINTをそれぞれ把握してまいりましょう!
・高度間隔ごとに一定の比率で減少
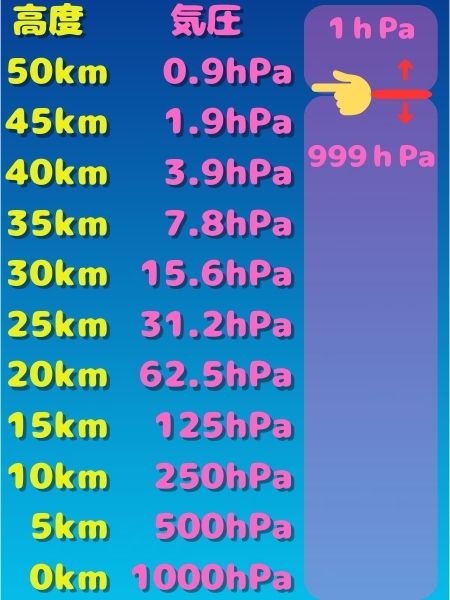
「高度が約5km上がるごとに気圧が半減」している状態を数値で確認してみましょう。
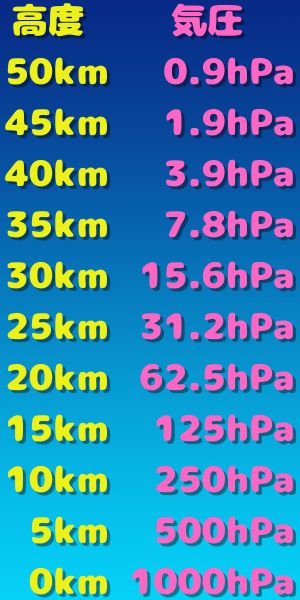
下層から上層に向かって
高度は上がり(5kmごと)
気圧は減少して(半減)
ゆく図となっております。
※高度5kmごとに、気圧は半減させており小数第2位以下は切り捨てております。
※問題を解くために数値化しており、自然界ではこれはあくまで目安の数値でございます。
※自然界において、実際の高度と気圧が正確にこの数値となるわけではございません。
これをふまえて、このまま次のポイントを確認してまいりましょう。
・大気全体の質量の99.9%
「大気全体の質量の99.9%」が何を意味しているのかを把握しましょう。
問題文には「~99.9%が含まれる地上からの平均的な高度」を求めています。
この地上からの99.9%の大気の質量を求めればよいのです。
そしてこの大気の質量が気圧のことなのです。
気圧:大気の圧力。通常、ある地点の気圧はその点を中心とする単位面積上で
気圧配置 気圧・高気圧・低気圧に関する用語|気象庁
その上の空気柱の総重量が相当する。単位はhPa(ヘクトパスカル)を使用する。
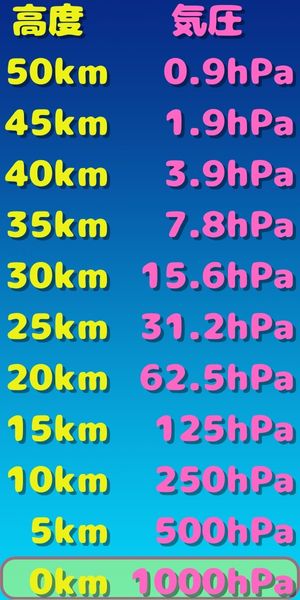
高度0kmが地上気圧です。
問題文より地上気圧は1000hPaです。
地上から上層の全ての大気の重さが
地上で1000hPaということです。
この全てが100%ということです。
$$100% = 1000hPa$$
それでは、「地上からの99.9%の大気の質量」を求めてみましょう。
$$99.9% = ? hPa$$
1000hPaの99.9%を求めるために下記の計算をするだけです。
$$1000(hPa)\times99.9(%)\times\frac{1}{100}=999(hPa)$$
・99.9%(999hPa)と0.01%(1hPa)の高度
それではいよいよ大気全体の質量の99.9%が含まれる地上から平均的な高度を求めましょう。
$$1000hPa(100%)-999hPa(99%)=1hPa(1%)$$
地上から大気の全体(100%)の質量(1000hPa)の
99.9%(999hPa)が含まれている高度より上の
大気の質量は0.1%(1hPa)となります。
したがって、「大気全体の質量の99.9%(999hPa)が含まれる地上から平均的な高度を求める」ことは1hPaの大気圧がかかっている高度を求めればよいのです。
$50km \fallingdotseq 0.9hPa$ より低く
$45km \fallingdotseq 1.9hPa$ より高い
上記条件を満たしている高度は、回答の選択肢の中では③48kmとなります。

実際の試験では時間との勝負の側面もあるため、今回の解説のような細かな計算は必要ないでしょう。
しっかりと内容を把握していただけるようにあえて細かな説明をさせていただきました!
問1/答え
③ 約48km
問2

問2/解説
- 「乾燥断熱減率[10℃/km]」と「湿潤断熱減率[5℃/km]」
- 「持ち上げ凝結高度」と「自由対流高度」

まずはじめに上記のPOINTにあげた、それぞれのワードの意味を確認してまいりましょう!
・乾燥断熱減率
未飽和の状態で空気塊が上昇する際の気温減率(どのぐらいの割合で気温が下がるか)です。
10℃/km (1℃/100m)
[10℃/km]とのことなので、1km上昇したときに10℃気温が下がるということですね。
割合としましては、100m上昇したときに1℃気温が下がるということですね。
・湿潤断熱減率
飽和した状態で空気塊が上昇する際の気温減率(どのぐらいの割合で気温が下がるか)です。
割合として乾燥断熱減率より小さくなる理由としましては、水蒸気が凝結する際に放出される潜熱があるからです。放出された潜熱が空気塊を暖める分、乾燥断熱減率より気温が下がりにくいんですね。
5℃/km (0.5℃/100m)
[5℃/km]とのことなので、1km上昇したときに5℃気温が下がるということですね。
割合としましては、100m上昇したときに0.5℃気温が下がるということですね。
それでは、これを踏まえまして、乾燥断熱減率と湿潤断熱減率をグラフ上でその傾き具合を確認しておきましょう。

乾燥断熱線と湿潤断熱線の傾きを視覚的にとらえていただくとよいですね。
●乾燥断熱線:空気塊が未飽和のとき乾燥断熱線に沿って上昇下降
●湿潤断熱線:空気塊が飽和しているとき湿潤断熱線に沿って上昇
上空に行くほど気温減率が大きくなるため、曲線を描いております。
※グラフはイメージです。正確な比率ではありません。
・持ち上げ凝結高度
地上の空気塊が断熱的に持ち上げられ、乾燥断熱線に沿って気温が下降し、空気塊がいよいよ飽和に達したときの高度。
そのため、持ち上げ凝結高度からさらに上昇する際の気温減率は湿潤断熱減率となるため、湿潤断熱線に沿って気温が下降して行くこととなります。
・自由対流高度
空気塊が周辺の大気の気温と等しくなる高度。自由対流高度を超えた空気塊は、周囲の大気より気温が高くなるので、空気塊が持ち上げられる要因がなくとも、自身の浮力によって上昇するのです。
(周りの空気の方が気温が低くて重く、空気塊の気温が相対的に高いので軽いといったイメージです!)
それでは、これを踏まえまして、先ほどの乾燥断熱減率と湿潤断熱減率も交えて、持ち上げ凝結高度と自由対流高度もグラフ上で確認しておきましょう。
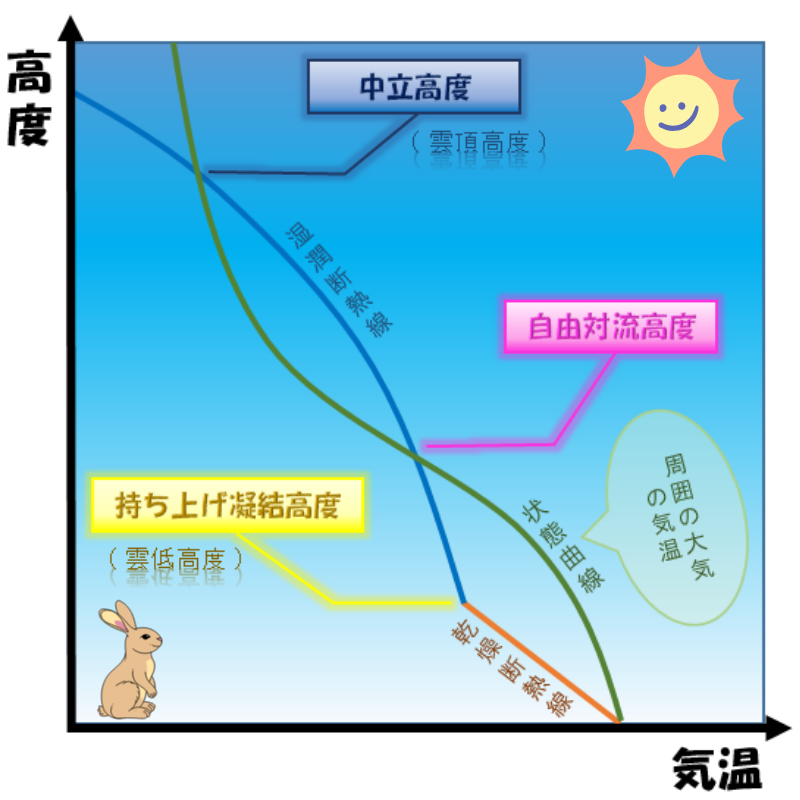
地上から空気塊が上昇する流れをグラフを基に見てゆきましょう!
①地上から乾燥断熱線に沿って気温が下降。
②飽和に達する高度が「持ち上げ凝結高度」。
③その後は湿潤断熱線に沿って気温が下降。
④周囲の大気と気温が等しくなる高度が「自由対流高度」。
それでは、あらためて問題文に指定されている気温や高度を上記グラフに当てはめて確認してみましょう。
地上(高度 0km)で気温が25℃、高度3kmで気温が5℃の大気中において、周囲の空気と混合せずに断熱的に地上から上昇した空気塊の自由対流高度が3kmとなった。
このとき、持ち上げ凝結高度は(a)km,そこでの空気塊の温度は(b)℃となる。
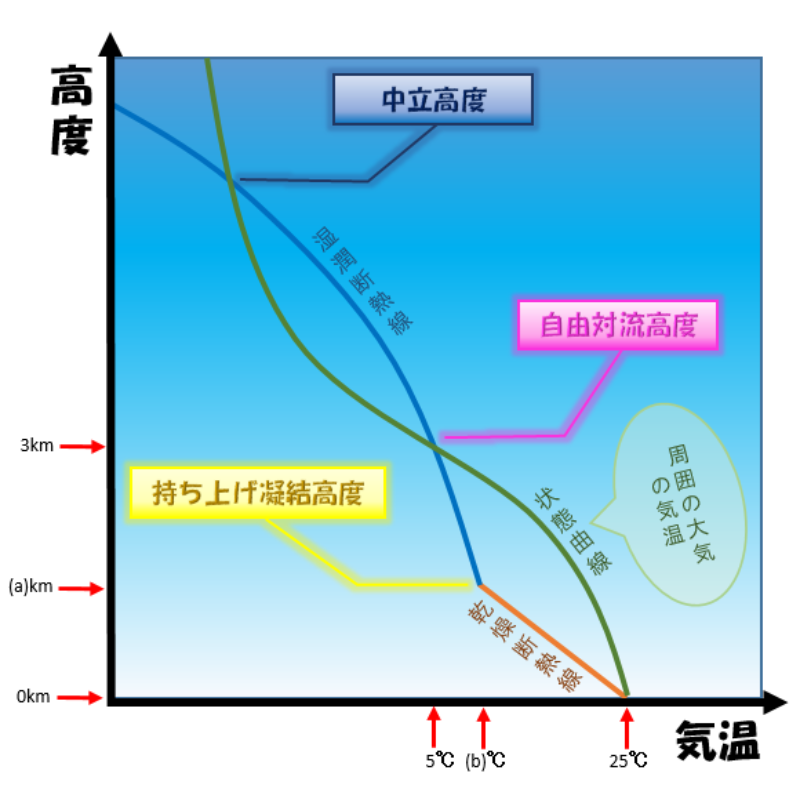
・地上(高度0km):25℃
[周囲の空気の温度/空気塊の温度]
・高度3km:5℃
[周囲の空気の温度]
・3km:自由対流高度
・(a)km:持ち上げ凝結高度
・(a)km:(b)℃
[空気塊の温度]
問題文の指定されている上記条件はヒントとなる数値です。これらを使って乾燥断熱減率と湿潤断熱減率を組み合わせれば、求めるべき持ち上げ凝結高度(a)kmとそこでの空気塊の温度(b)℃を導き出せます。
①[地上]から[持ち上げ凝結高度]まで
・温度:25℃から(b)℃まで下降 = 温度差:25℃-(b)℃
・高度:0kmから(a)kmまで上昇 = 高度差:(a)km-0km
・気温減率:10℃/km(乾燥断熱減率)
上記①の各条件より
[地上気温25℃から持ち上げ凝結高度の気温の差]=[持ち上げ凝結高度と地上の高度差分を乾燥断熱減率で下降する温度]
25℃–(b)℃={((a)km-0km)×10℃} ‥‥①
「持ち上げ凝結高度の気温」を求めるには、「地上の気温」から「持ち上げ凝結高度」までの高度分を「乾燥断熱減率」の割合で求めた気温の分だけ下降させると考えた方が自然な流れで式が立てやすいかもですね。
[持ち上げ凝結高度の気温]=[地上の気温]-[持ち上げ凝結高度×乾燥断熱減率]
(b)℃=25℃–{(a)km×10℃} ‥‥①
結局は同じ①の式を導き出しているので、どちらの考え方でも式を組み立てられればOKです!
②[持ち上げ凝結高度]から[自由対流高度]まで
・温度:(b)℃から5℃まで下降 = 温度差:(b)℃–5℃
・高度:(a)kmから3kmまで上昇 = 高度差:3km-(a)km
・気温減率:5℃/km(湿潤断熱減率)
上記②の各条件より
[自由対流高度の気温と持ち上げ凝結高度の気温の差]=[(自由対流高度と持ち上げ凝結高度の高度差分)を湿潤断熱減率で下降する温度]
(b)℃-5℃=(3km-(a)km)×5℃ ‥‥②
「自由対流高度の気温」を求めるには、「持ち上げ凝結高度の気温」から「持ち上げ凝結高度」と「自由対流高度」の高度差を「湿潤断熱減率」の割合で求めた気温の分だけ下降させると考えた方が自然な流れで式が立てやすいかもですね。
[自由対流高度の気温]=[持ち上げ凝結高度の気温]-[(自由対流高度)-(持ち上げ凝結高度)×湿潤断熱減率]
5℃=(b)℃-{(3km-(a)km)×5℃} ‥‥②
結局は同じ②の式を導き出しているので、どちらの考え方でも式を組み立てられればOKです!
あとは上記①と②の連立方程式を解くことで(a)と(b)を導き出せますね。
\begin{eqnarray} \left\{ \begin{array}{l}25- (b) =(a)×10\\(b)-5=(3-(a))×5\end{array} \right. \end{eqnarray}
\begin{eqnarray} \left\{ \begin{array}{l} (b) =25-(a)×10\\5=(b)-(3-(a))×5\end{array} \right. \end{eqnarray}
計算結果は、(a)=1、(b)=15となります。
持ち上げ凝結高度は(a)の1km,そこでの空気塊の温度は(b)の15℃を導き出せましたね!

各ワードの意味や空気塊の上昇時の気温減率の流れなどをしっかりと把握していただけるようにあえて細かな説明をさせていただきました!
実際の試験では、最後の①と②の連立方程式をすぐに導き出して計算をしてあげればよいので、今回の解説量ほどは時間をかけずに解答を導きだせるようにしておきましょう!
問2/答え
② 1 15
問3

問3/解説
- 「飽和水蒸気圧」を理解しよう!
- 「飽和混合比」を理解しよう

まずはじめに上記のPOINTにあげた、それぞれのワードの意味を確認してまいりましょう!
・飽和水蒸気圧
まずは「水蒸気圧」を理解しましょう。
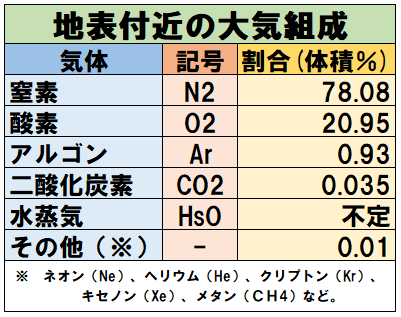
地球の大気は「酸素」や「二酸化炭素」以外にも「窒素」や「アルゴン」など、いろいろな成分で構成されております。
それらの構成成分の中に「水蒸気」も含まれております。
それぞれの気体分子の圧力を分圧といって、すべての気体分子の分圧の和が大気圧ということになります。その分圧のうち、水蒸気分子による分圧が水蒸気圧です。
これらを踏まえていよいよ「飽和水蒸気圧」を理解いたしましょう。
空気の中にどれだけ水蒸気が含まれているかは、その空気の状態によります。
その空気がめいいっぱい水蒸気を含んだ時の水蒸気圧が飽和水蒸気圧となります。
同じ温度の場合
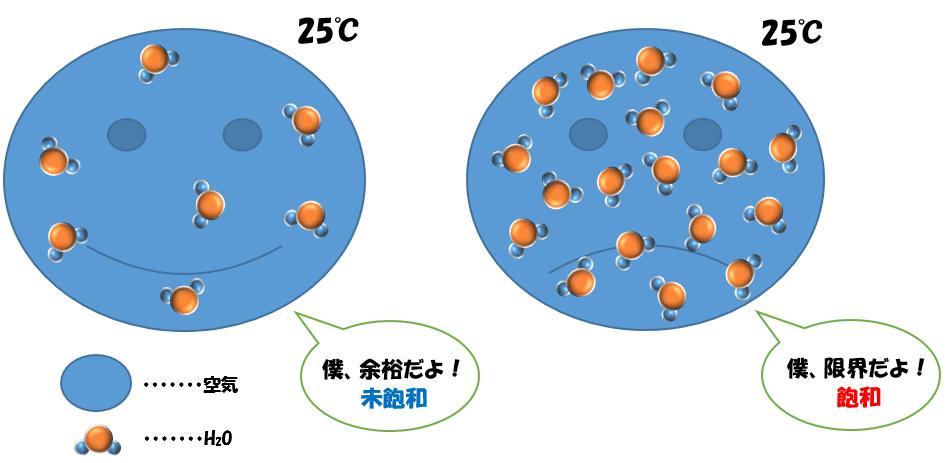
そして、この飽和水蒸気圧は空気の気温が高くなるほど大きくなっているのです!

異なる温度の場合
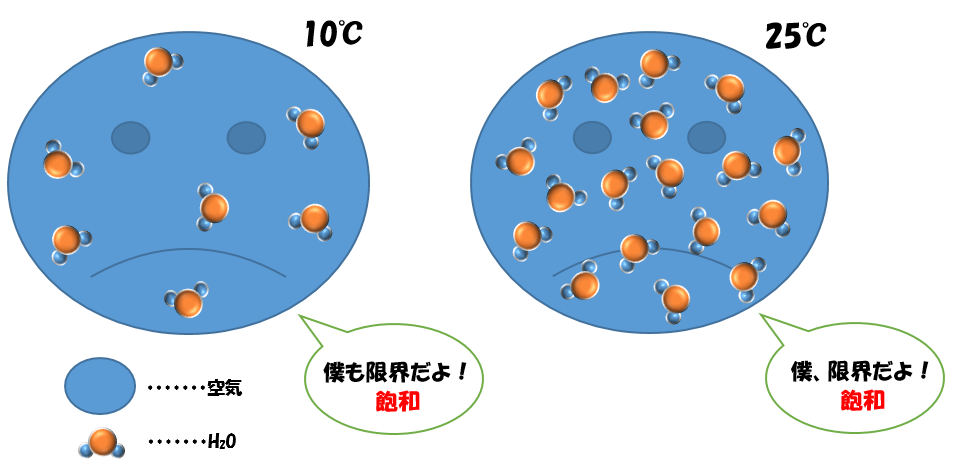
覚えておいていただきたいのは「飽和水蒸気圧は大気の気温によって決まる。」ということです!
・飽和混合比
つぎに「混合比」を理解しましょう。
まず「乾燥空気」に対して「湿潤空気」といいますが、
「乾燥空気」は水蒸気を含まない空気、
「湿潤空気」は水蒸気を含む空気のことです。
この「湿潤空気」に含まれる「乾燥空気の質量」に対する「水蒸気の質量」の比のことを「混合比」といいます。
$$混合比W=\frac{水蒸気の質量}{乾燥空気の質量}$$
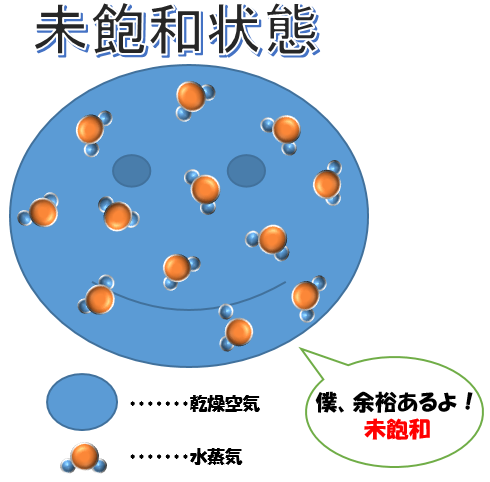
そしてこの空気塊が飽和している状態の混合比を「飽和混合比」といいます。
$$飽和混合比W=\frac{水蒸気の質量}{乾燥空気の質量}$$
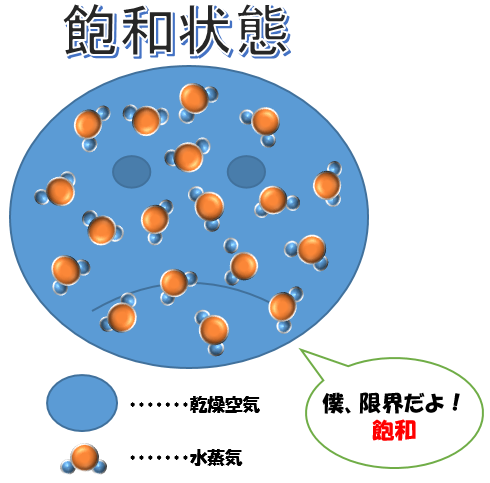
さらに質量(m)は密度(ρ)と体積(v)の積であるため(m=ρv)であり、単位体積(v=1m3)でみるとm=ρ(質量=密度)となるため、混合比(w)は「乾燥空気の密度(ρd)」に対する「水蒸気の密度(ρv)」の比とも等しくなります。
$$w=\frac{ρ_v}{ρ_d}$$
そして今回の問題を解くにあたっては混合比(w)を「湿潤空気の圧力(P[hPa])」と「水蒸気圧(e[hPa])」の関係式として下記の近似式が成り立つことを知っておく必要があります。
$$w=0.622\times\frac{e}{P}$$

上記関係式の導き方は知っておくと良いかもですが、頭がこんがらがっちゃうって方はいったん下記の「混合比を求める近似式」は覗かないほうが良いかもです(笑)
どうしても理解しておきたいって方は「▶」をクリックしてみてください。
混合比を求める近似式
・上で説明したように混合比(w)は「乾燥空気の密度(ρd)」に対する「水蒸気の密度(ρv)」の比と等しくなります。
$$w=\frac{ρ_v}{ρ_d} …①$$
$$w:混合比 $$$$ρ_v:水蒸気密度 $$$$ρ_d:乾燥空気の密度$$
・ここで気体の状態方程式を思い出してください。
$$P=ρRT$$
$$P:気体の圧力 $$$$ρ:密度 $$$$R:気体定数 $$$$T:温度 $$
・ここで「乾燥空気の分圧」と「水蒸気圧」をそれぞれの気体の状態方程式であらわします。
$$P_d=ρ_dR_dT$$
↓
$$ρ_d=\frac{P_d}{R_dT} …②$$
$$P_d:乾燥空気の分圧 $$$$ρ_d:乾燥空気の密度 $$$$R_d:乾燥空気の気体定数$$$$T:温度 $$
$$e=ρ_vR_vT$$
↓
$$ρ_v=\frac{e}{R_vT} …③$$
$$e:水蒸気の分圧(水蒸気圧) $$$$ρ_v:水蒸気の密度 $$$$R_v:水蒸気の気体定数 $$$$T:温度 $$
・そして、「空気塊(湿潤空気)の気圧」は「乾燥空気の分圧」と「水蒸気の分圧」の和ですね。
$$P=P_d+e$$
↓
$$P_d=P-e …④$$
$$P:空気塊(湿潤空気)の気圧 $$$$P_d:乾燥空気の分圧 $$$$e:水蒸気の分圧(水蒸気圧) $$
・①の式に②と③の式を代入いたします。
$$w=\frac{ρ_v}{ρ_d}=\frac{\frac{e}{R_vT}}{\frac{P_d}{R_dT}}=\frac{eR_dT}{P_dR_vT}=\frac{R_d}{R_v}\times\frac{e}{P_d}$$
・上記式に④を代入し「乾燥空気の気体定数」と「水蒸気の気体定数」の各数値を代入します。
$$w=\frac{R_d}{R_v}\times\frac{e}{P_d}$$
↓
$$w=\frac{287.0}{461.5}\times\frac{e}{P-e}$$
↓
$$w\fallingdotseq0.622\times\frac{e}{P-e}$$
乾燥空気の気体定数
$$R_d=287.0m^{2}s^{-2}K^{-1}$$
水蒸気の気体定数
$$R_v=461.5m^{2}s^{-2}K^{-1}$$
・水蒸気は一般的に空気中で0〜4%まで変動します。「水蒸気圧e」は0~0.04気圧の幅にあります。
「気体の圧力P」のうち「水蒸気の分圧(水蒸気圧)e」は0.04を超えることがないことを表すと下記になります。
$$\frac{e}{P}\lt0.04$$
↓
$$e\lt0.04P$$
$$P:空気塊の気圧 $$$$e:水蒸気の分圧(水蒸気圧)$$
・このように「水蒸気圧e」は「気体の圧力P」に比べて十分に小さい値であることが確認できました。
・ここで下記式の右辺の分母の「P-e」のうち「水蒸気圧e」を無視することで最終的に近似式をえることができるのです。
$$w\fallingdotseq0.622\times\frac{e}{P-e}$$
↓
$$w\fallingdotseq0.622\times\frac{e}{P}$$
$$w:混合比 $$$$P:空気塊の気圧 $$$$e:水蒸気の分圧(水蒸気圧)$$
以上でポイントとして挙げた「飽和水蒸気圧」と「飽和混合比」はご理解いただけたでしょうか!
それではこれを踏まえまして、いよいよ問題をひとつひとつ確認してまいりましょう!
まずは各設問に対して下記「A」と「B」が比較対象として条件設定されております。
A:気圧850hPa、温度5℃の空気塊の飽和水蒸気圧
B:気圧850hPa、温度5℃の空気塊の飽和混合比
(a)気圧850hPa、温度5℃の空気塊の飽和水上気圧はAよりも大きい。
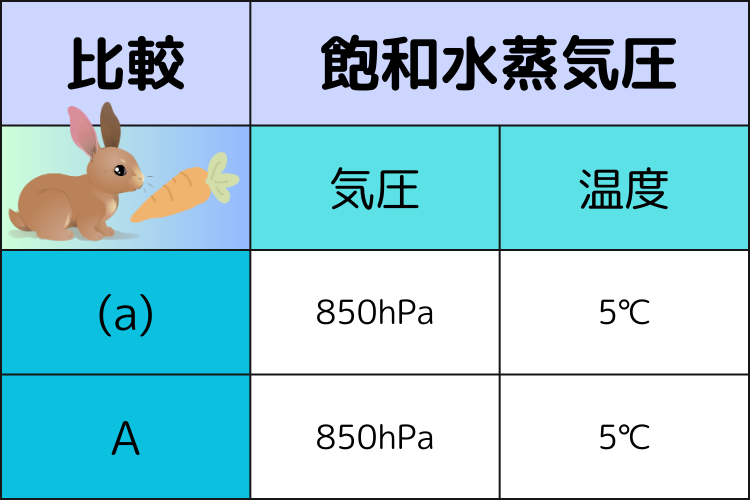
(a)の設問は「飽和水蒸気圧」が比較対象となっているため、ポイントは「温度」です。
「飽和水蒸気圧は大気の気温によって決まる。」
(a)の空気塊の温度とAの温度はともに「5℃」で同じです!
「飽和水蒸気圧は大気の気温によって決まる。」ため、5℃=5℃より下記の比較が可能となります。
$$e_{(a)} = A$$
$$e_{(a)}:(a)の空気塊の飽和水蒸気圧 $$$$A:問3の飽和水蒸気圧 $$
したがって温度が同じであるため飽和水蒸気圧も同じとなります!
正)気圧850hPa、温度5℃の空気塊の飽和水上気圧はAと同じ。
したがって(a)の文章は「誤」となります!
(b)気圧850hPa、温度10℃の空気塊の飽和混合比はBよりも大きい。
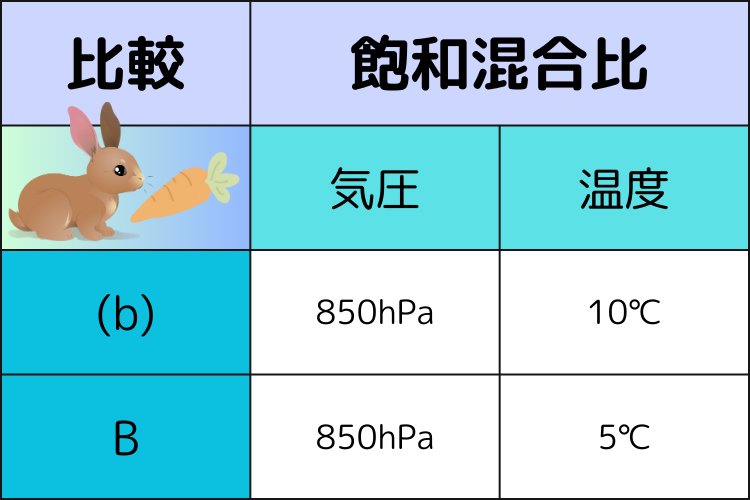
(b)の設問は「飽和混合比」が比較対象となっているため、下記混合比の近似式より、「気圧」や「温度」の値にて比較可能となります。
$$w=0.622\times\frac{e}{P}$$
(b)の空気塊と問3の空気塊の唯一の相違点が温度で「10℃」と「5℃」です。
「飽和水蒸気圧は大気の気温によって決まる。」ため、10℃>5℃より下記の比較が可能となります。
$$e_{(b)} \gt e_B$$
$$e_{(b)}:(b)の空気塊の飽和水蒸気圧 $$$$e_B:問3の飽和水蒸気圧(A) $$
混合比の近似式より、水蒸気圧は右辺の分子にあるため、水蒸気圧が大きい方が混合比の値も大きくなります。
$$w_{(b)}=0.622\times\frac{e_{(b)}}{850hPa} \gt w_B=0.622\times\frac{e_B}{850hPa}$$
したがって温度が高い(b)の飽和混合比のほうが大きくなります!
正)気圧850hPa、温度10℃の空気塊の飽和水上気圧はBよりも大きい。
したがって(b)の文章は「正」となります!
(c)気圧900hPa、温度5℃の空気塊の飽和混合比はBよりも大きい。
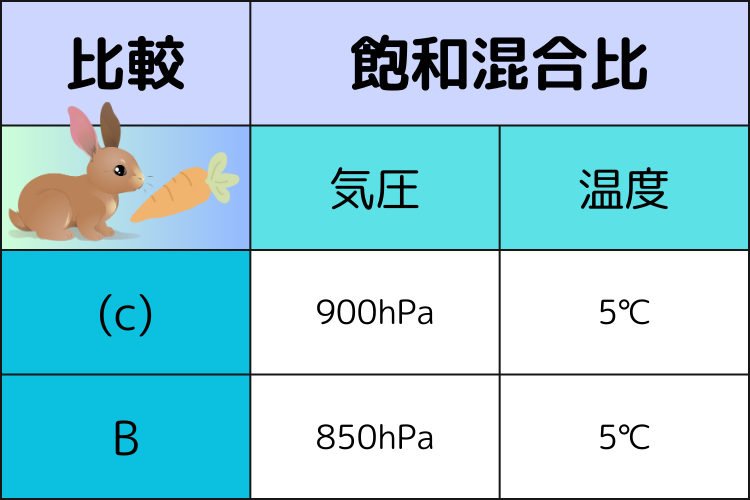
(c)の設問は「飽和混合比」が比較対象となっているため、下記混合比の近似式より、「気圧」や「温度」の値にて比較可能となります。
$$w=0.622\times\frac{e}{P}$$
(c)の空気塊と問3の空気塊の唯一の相違点が気圧で「900hPa」と「850hPa」です。
「飽和水蒸気圧は大気の気温によって決まる。」ため、5℃=5℃より下記の比較が可能となります。
$$e_{(c)} = e_B$$
$$e_{(c)}:(c)の空気塊の飽和水蒸気圧 $$$$e_B:問3の飽和水蒸気圧(A) $$
混合比の近似式より、気圧は右辺の分母にあるため、気圧が大きい方が混合比の値は小さくなります。
$$w_{(b)}=0.622\times\frac{e_{(c)}}{900hPa} \lt w_B=0.622\times\frac{e_B}{850hPa}$$
したがって気圧が高い(c)の飽和混合比のほうが小さくなります!
誤)気圧900hPa、温度5℃の空気塊の飽和水上気圧はBよりも大きい。
したがって(c)の文章は「誤」となります!
答えは「(a)誤 (b)正 (c)誤」となり④が正解となりますね。

「飽和水蒸気圧」と「混合比」をご理解いただくために、あえて事細かに説明をさせていただきました。実際のところは「飽和水蒸気圧は大気の気温によって決まる。」ことと下記の「混合比の近似式」を御存知であれば、ここまで複雑に考えなくても解ける問題ではあるかと思われます。実際の試験では極力時間をかけずにシンプルに考えて解答を導きましょう!
$$w=0.622\times\frac{e}{P}$$
問3/答え
④ 誤 正 誤
問4

問4/解説
- 「水滴の成長」のうち「凝結過程」と「併合過程」のそれぞれの特徴を把握しておこう!
- 「冷たい雨」と「暖かい雨」のそれぞれの特徴を把握しておこう!
- 「直径が8mmを超える雨粒は地上では観測されていない」ことを知っておこう!

問4の問題はどちらかというと考えて答えを導き出すというよりは「知っているか、知らなかったか」を問われている知識の問題ですね。過去問に出てくる問題の知識は100%身につけておきましょう!
・凝結過程
雲粒(水滴)の表面に過飽和の状態にある周囲の水滴が凝結して雲粒(水滴)が成長して行く過程。
・併合過程
雲粒(水滴)同士が衝突して併合することで雲粒(水滴)が成長して行く過程。
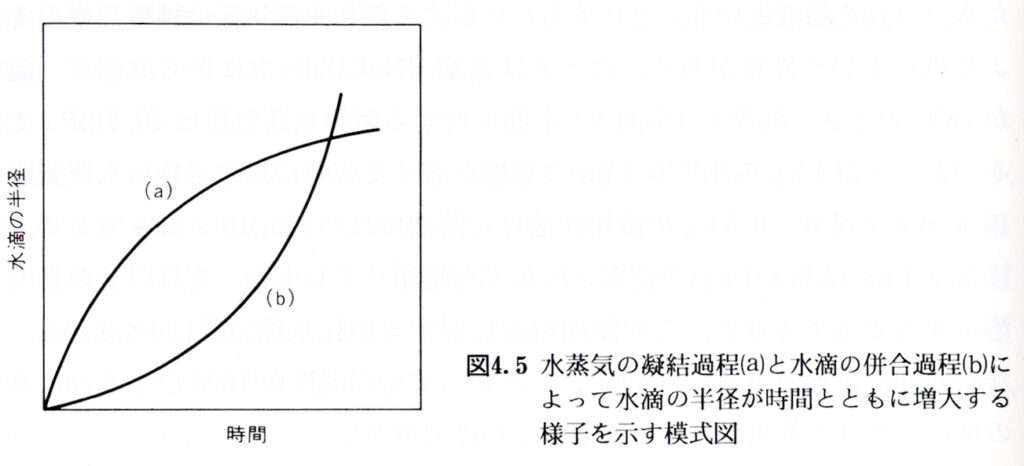
そして、(a)と(b)に関しては下記のグラフを頭の片隅に記憶しておくことで対応しましょう。
一般気象学【第2版】|小倉義光
(a)水蒸気の凝結による水滴の成長過程では、水滴の半径が小さいほど単位時間の半径の増加率は大きい。
(a)に関しては「凝結過程」の水滴の成長に関してですね。
上記グラフより「凝結過程」によって「水滴の半径が時間とともに増大する」のみを見てみると。
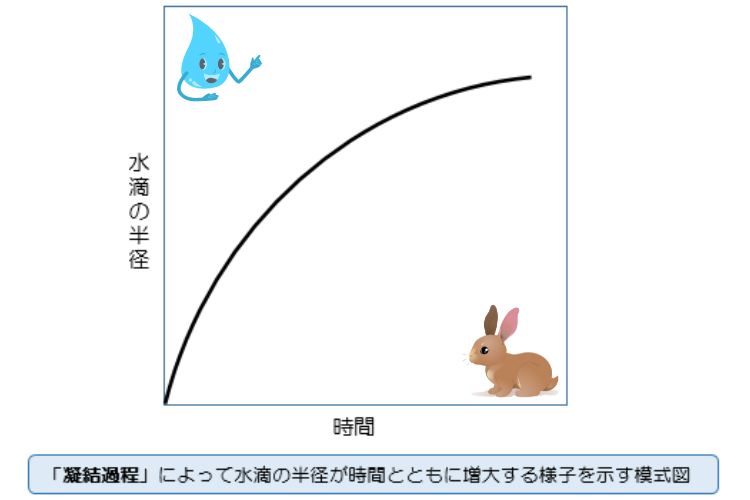
このグラフからも確認できる通り「水滴の半径が小さい」ほうが「半径の増加率は大きい」
ことが確認できます。
したがって(a)は「正」となります!
さらに言うと「水滴の半径が大きくなる」⇒「半径の増加率が小さくなる」ということですね。
よって「凝結過程」による雨粒の成長はある程度の大きさからはなかなか成長しなくなります。
そこで次なるステップとして「併合過程」による成長で雨粒はさらに成長して行くことになります!
(b)水滴同士が衝突・併合して成長する過程では、一般的に水滴が大きく成長するにつれて単位時間の半径の増加率は小さくなる。
(b)に関しては「併合過程」の水滴の成長に関してですね。
上記グラフより「併合過程」によって「水滴の半径が時間とともに増大する」のみを見てみると。
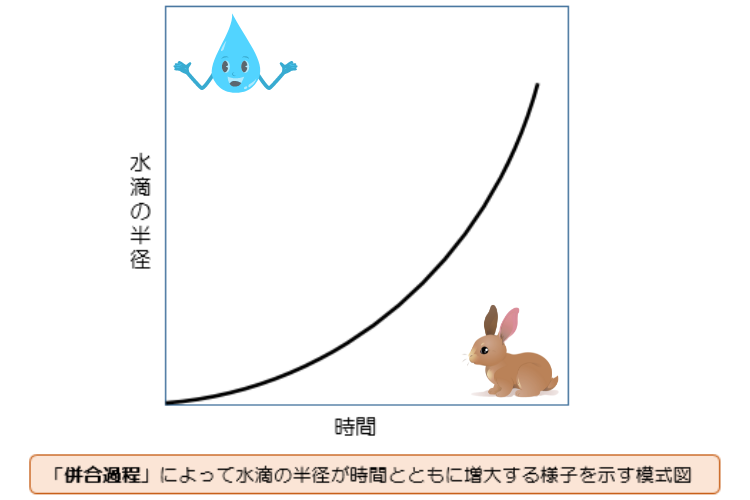
このグラフからも確認できる通り「水滴の半径が大きなるほど」⇒「半径の増加率は大きくなる」
ことが確認できます。
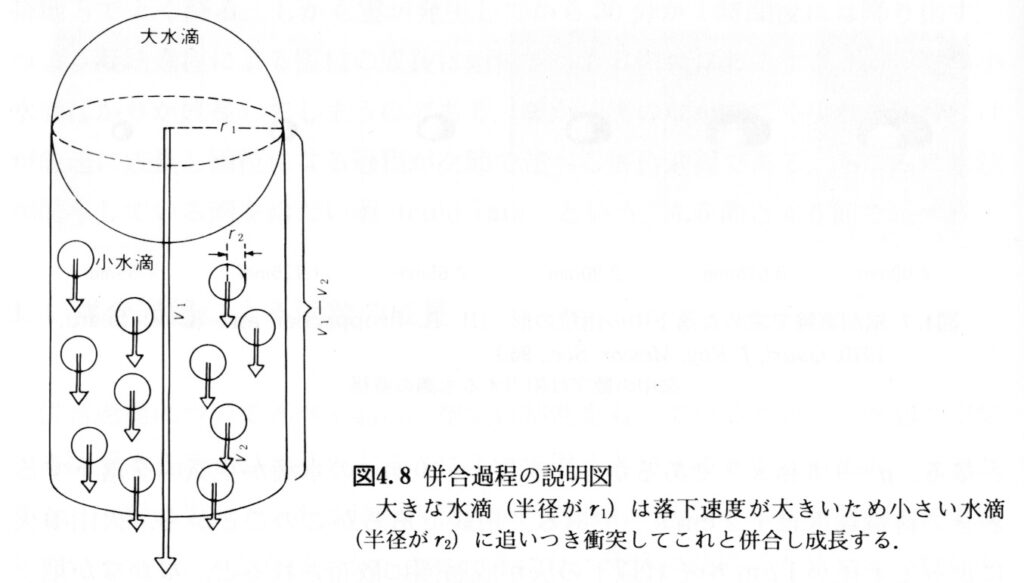
また、併合過程による水滴の成長に関しては、下記の図も頭の片隅に記憶しておきましょう!
一般気象学【第2版】|小倉義光
上記図よりイメージできることは、「大水滴」が大きくなればなるほど、
・落下速度が大きくなる⇒たくさんの小水滴に追いつきやすくなる
・大水滴の断面積が大きくなる⇒たくさんの小水滴に衝突しやくすくなる
この図からも「水滴の半径が大きなるほど」⇒「半径の増加率は大きくなる」ことが確認できます。
したがって(b)は「誤」となります!
(c)暖かい雨の形成過程における水蒸気の凝結と水滴同士の衝突・併合による水滴の成長はともに遅く、水滴が成長して降水がはじまるまでに1時間以上かかる。
まずは「冷たい雨」と「暖かい雨」とはどんな雨なのかをさくっと確認しておきましょう。
冷たい雨
・水蒸気が凝結して雲粒となり、さらに雲の中で氷粒となり、地表に落下する際に融けて降る雨のこと。
・中緯度帯の降水は冷たい雨がほとんどである。
暖かい雨
・雲の中の温度が0℃以下にならない場合、凝結した雲粒が氷粒とならず、そのまま地表に降るあめのこと。
・熱帯地方の降水は暖かい雨となることが多い。
そして、「一般気象学」の暖かい雨の説明の箇所には下記のような説明が記載されております。
(c)の問題はこの「暖かい雨」の特徴を把握しておくことが必須です。
一般に雲の中の温度が0℃より高く氷粒を含んでいないような雲を暖かい雲という。
一般気象学【第2版】|小倉義光
そのような雲からでも雨はよく降る。これを暖かい雨と言い、熱帯地方で良く降る。
しかも雲が発生してから30分か1時間後には降りだす。
(c)の問題を熱帯地方では暖かい雨が良く降るといった側面から見てゆくと、
熱帯地方⇒気温が高い⇒飽和水蒸気圧が高い⇒水面(海面等)からの蒸発量が多い⇒絶対湿度が高い
└凝結する水蒸気が多い ⇒ 衝突する雲粒が多い ⇒ 併合過程での成長が助長される
└雲粒の多い中での併合過程による成長は加速度的に早くなる
気温が0℃以下へ低下する高度よりも下層の大気中で、上記の併合過程による成長によって雨粒となり、暖かい雨が降ることになる訳です。
そのため、暖かい雨は凝結と水滴同士の衝突・併合による水滴の成長はともに早く、「一般気象学」で説明されているように、雲が発生してから30分から1時間後には降りだす雨となるのです。
したがって(c)は「誤」となります!
(d)積乱雲の中では強い鉛直流の中で短時間のうちに水滴が大きく成長し、水滴の直径が10mmを超えることがある。
雨粒、ここでいう「水滴」の直径が無限大に大きくならないことは、誰もが経験則的に知っていることだと思います。例えば水滴の直径が「5cmを超えることがある」なんて問題であれば簡単なのですが、
今回のように「10mm」となるとなかなか微妙な大きさで、実際に雨粒の直径を測る機会もないので、なおさら経験則からは判断ができない人がほとんどでしょう。
水滴の大きさには「表面張力」が関係しております。
「表面張力」とは水滴の表面積を最小にするように働く力のことです。
最小にするということは「球」の形を保とうとすることです。
ところが逆に水滴自体が大きくなると、この表面張力が相対的に小さくなってゆきます。
さらに大きくなった水滴は落下中には空気抵抗を受けるため、ますます球形ではいられなくなります。

この時点で水滴は分裂してしまったり、実際には水滴同士が衝突することで大きな水滴は分裂してしまうようです。このことを踏まえて、地上では8mmを超えた雨粒は観測されていないことを知識として持っておきましょう。
したがって(d)は「誤」となります!
問4/答え
③ 正 誤 誤 誤
問5


問5/解説
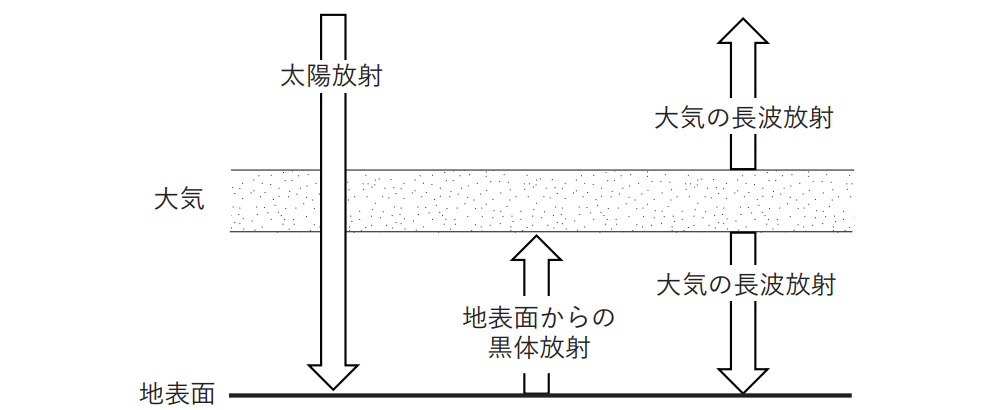
- 「黒体放射」がどのようなものであるかを把握しておこう!
- 「ステファン・ボルツマンの式」を理解しておこう!
- 「太陽放射(短波放射)」「地球放射(長波放射)」など放射の定義を整理しておこう!

問5の問題はステファン・ボルツマンの法則を使って、温室効果なるものを確認する問題だね。
解説ではこの法則を使って一つ一つの設問を確認して行くけれど、ステファンボルツマンの法則と温室効果を把握していれば、実は今回の問題は消去法から答えは導けてしまうんだ。
しかし、今後のため、応用力を養うためにも、しっかり理解と把握をしておきましょう!
温室効果を説明する文章の初めの部分は、「地球に大気がないとき」とのこと。
これは「温室効果の気体(大気)」がないときと、文章の後半のあるときを比較して説明するための導入部分ですね。
問題の図を基に、大気がないときの図に書き換えて、問題文にある放射平衡状態と地表面温度を確認してみましょう。
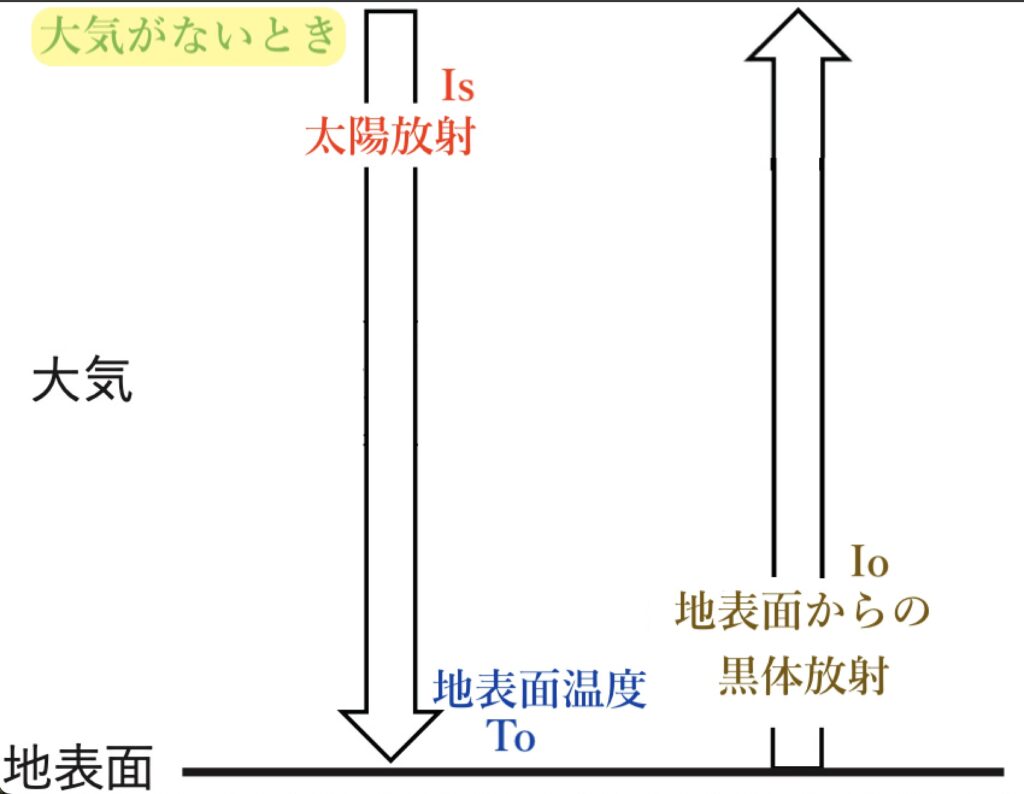
- Is=太陽放射
- I0=地表面からの黒体放射
- T0=地表面温度
問題文の条件に「地表面は黒体で全ての放射を完全に吸収する。」とある。
ここで「黒体放射」がどのようなものであるかを再確認してみましょう。
問5/答え
② 正 正 誤 誤
問6

問6/解説
鋭意作成中
問6/答え
④ 1.4
問7


問7/解説
鋭意作成中
問7/答え
① 正 負 正 正
問8

問8/解説
鋭意作成中
問8/答え
⑤ 誤 正 正 誤
問9


問9/解説
鋭意作成中
問9/答え
③ 誤 正 誤 正
問10

問10/解説
鋭意作成中
問10/答え
② 正 誤 正 誤
問11

問11/解説
鋭意作成中
問11/答え
⑤ 誤 誤 誤 正
問12

問12/解説
鋭意作成中
問12/答え
① (a)のみ誤り
問13

問13/解説
鋭意作成中
問13/答え
⑤ 誤 誤 正 誤
問14

問14/解説
鋭意作成中
問14/答え
④ 誤 誤 正 正
問15

問15/解説
鋭意作成中
問15/答え
⑤ すべて正しい